Advertisements
Advertisements
Question
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
Solution
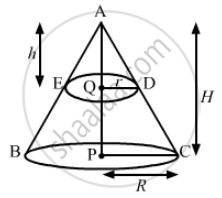
We have,
Radius of solid cone, R = CP = 10 cm,
Let the height of the solid cone be, AP = H,
the radius of the smaller cone, QD = r and
the height of the smaller cone be, AQ = h.
Also,
Now, in Δ AQD and Δ APC
∠QAD = ∠PAC (Common angle)
∠AQD = ∠APC = 90°
So, by AA criteria
ΔAQD ˜ ΔAPC
As,
Volume of smaller cone
And,
Volume of solid cone
so, Volume frustum = Volume of solid cone - Volume of smaller cone
Now, the ratio of the volumes of the two parts
= 1 : 7
So, the ratio of the volume of the two parts of the cone is 1 : 7.
APPEARS IN
RELATED QUESTIONS
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
A cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. the whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
The diameter of a sphere is 6 cm. It is melted and drawn in to a wire of diameter 2 mm. The length of the wire is
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
Match the column:
| (1) surface area of cuboid | (A) πr2h |
| (2) surface area of closed right cylinder | (B) 2πr(h + r) |
| (3) Total surface area of right cone | (C) πrl + πr2 |
| (4) Total surface area of hemisphere | (D) 3πr3 |
| (E) 3πr2 | |
| (F) 2[lb + bh + lh] |
The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
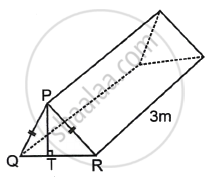
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent