Advertisements
Advertisements
Question
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
Solution
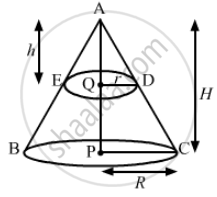
We have,
Height of the given cone, H = 20 cm
Let the radius of the given cone be h and
the height of the smaller cone be r.
Now, in ΔAQD and ΔAPC,
∠QAD = ∠PAC (Common angle)
∠AQD = ∠APC = 90°
So, by AA criteria
∠AQD ˜∠APC
`rArr ("AQ")/"AP"=("QD")/("PC")`
`rArr "h"/"H" = "r"/"R" .......(i)`
Volume of smaller cone `= 1/8xx "Volume of the given cone"`
`rArr "Volume of smaller cone"/"Volume of the given one" = 1/8`
`rArr ((1/3pi"r"^2"h"))/((1/3pi"R"^2"H"))=1/8`
`rArr ("r"/"R")^2xx("h"/"H") = 1/8`
`rArr ("h"/"H")^2xx("h"/"H")=1/8` [Using (i)]
`rArr ("h"/"H")^3 = 1/8`
`rArr "h"/"H"=root(3)(1/8)`
`rArr "h"/"20" = 1/2`
`rArr "h" = 20/2`
`rArr "h" = 10 "cm"`
∴ PQ = H - h = 20 - 10 cm
So, the section is made at the height of 10 cm above the base.
APPEARS IN
RELATED QUESTIONS
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area.
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum?
A cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A shuttlecock used for playing badminton has the shape of the combination of ______.
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
A shuttle cock used for playing badminton has the shape of a combination of ______.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
