Advertisements
Advertisements
Question
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
Solution
Radius of the cone, R = 4 cm
Let the height be H.
Since the plane divides the cone into two parts through the mid point so, a small cone and a frustum will be formed.
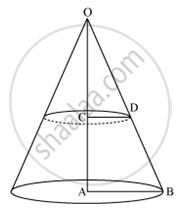
\[OC = CA = \frac{H}{2}\]
Let the radius of the smaller cone be r cm.
In ∆OCD and ∆OAB,
∠OCD = ∠OAB (90°)
∠COD = ∠AOB (Common)
∴∆OCD ∼ ∆OAB (AA Similarly criterion)
\[\Rightarrow \frac{OA}{OC} = \frac{AB}{CD} = \frac{OB}{OD} \left( \text { corresponding sides are proportional } \right)\]
\[ \Rightarrow \frac{H}{\frac{H}{2}} = \frac{4}{r}\]
\[ \Rightarrow r = 2 cm\]
Now volume of the smaller cone = \[\frac{1}{3}\pi \left( CD \right)^2 \times OC = \frac{1}{3}\pi \left( 2 \right)^2 \times \frac{H}{2} = \frac{2\pi H}{3} cm\]
Height of the frustum of the cone = \[\frac{H}{2}\]
Volume of frustum of cone = \[\frac{1}{3}\pi h\left[ r_1^2 + r_1 r_2 + r_2^2 \right]\]
\[= \frac{1}{3}\pi\left( \frac{H}{2} \right)\left[ \left( 4 \right)^2 + \left( 2 \right)^2 + 4 \times 2 \right]\]
\[ = \frac{14\pi H}{3} {cm}^3\]
\[\frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{\frac{2\pi H}{3}}{\frac{14\pi H}{3}}\]
\[ \Rightarrow \frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{1}{7}\]
Hence, the ratio of the volumes of the two parts will be 1 : 7.
APPEARS IN
RELATED QUESTIONS
Derive the formula for the curved surface area and total surface area of the frustum of cone.
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
In a right circular cone , the cross-section made by a plane parallel to the base is a
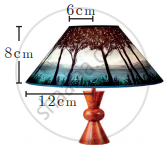
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.
The slant height of the frustum of a cone having radii of two ends as 5 cm and 2 cm respectively and height 4 cm is ______.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm, respectively. Find the height of the bucket.
