Advertisements
Advertisements
प्रश्न
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
उत्तर
Radius of the cone, R = 4 cm
Let the height be H.
Since the plane divides the cone into two parts through the mid point so, a small cone and a frustum will be formed.
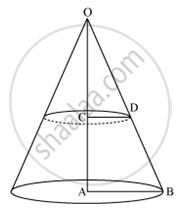
\[OC = CA = \frac{H}{2}\]
Let the radius of the smaller cone be r cm.
In ∆OCD and ∆OAB,
∠OCD = ∠OAB (90°)
∠COD = ∠AOB (Common)
∴∆OCD ∼ ∆OAB (AA Similarly criterion)
\[\Rightarrow \frac{OA}{OC} = \frac{AB}{CD} = \frac{OB}{OD} \left( \text { corresponding sides are proportional } \right)\]
\[ \Rightarrow \frac{H}{\frac{H}{2}} = \frac{4}{r}\]
\[ \Rightarrow r = 2 cm\]
Now volume of the smaller cone = \[\frac{1}{3}\pi \left( CD \right)^2 \times OC = \frac{1}{3}\pi \left( 2 \right)^2 \times \frac{H}{2} = \frac{2\pi H}{3} cm\]
Height of the frustum of the cone = \[\frac{H}{2}\]
Volume of frustum of cone = \[\frac{1}{3}\pi h\left[ r_1^2 + r_1 r_2 + r_2^2 \right]\]
\[= \frac{1}{3}\pi\left( \frac{H}{2} \right)\left[ \left( 4 \right)^2 + \left( 2 \right)^2 + 4 \times 2 \right]\]
\[ = \frac{14\pi H}{3} {cm}^3\]
\[\frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{\frac{2\pi H}{3}}{\frac{14\pi H}{3}}\]
\[ \Rightarrow \frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{1}{7}\]
Hence, the ratio of the volumes of the two parts will be 1 : 7.
APPEARS IN
संबंधित प्रश्न
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is `1/27` of the given cone, then at what height it is cut from its base?
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container , at thr rate of ₹25 per litre. (Use \[\pi = 3 . 14) .\]
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A frustum of a cone is 9 cm thick and the diameters of its circular ends are 28 cm and 4 cm. Find the volume and lateral surface area of the frustum.
(Take π = 22/7).
A bucket is in the form of a frustum of a cone and holds 15.25 litres of water. The diameters of the top and bottom are 25 cm and 20 cm respectively. Find its height and area of tin used in its construction.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water . The radii of the top and bottom are 28 cm and 21 cm respectively . Find the height of the bucket .
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
The frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹ 2.