Advertisements
Advertisements
प्रश्न
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
उत्तर
Radius of the cone, R = 4 cm
Let the height be H.
Since the plane divides the cone into two parts through the mid point so, a small cone and a frustum will be formed.
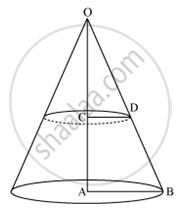
\[OC = CA = \frac{H}{2}\]
Let the radius of the smaller cone be r cm.
In ∆OCD and ∆OAB,
∠OCD = ∠OAB (90°)
∠COD = ∠AOB (Common)
∴∆OCD ∼ ∆OAB (AA Similarly criterion)
\[\Rightarrow \frac{OA}{OC} = \frac{AB}{CD} = \frac{OB}{OD} \left( \text { corresponding sides are proportional } \right)\]
\[ \Rightarrow \frac{H}{\frac{H}{2}} = \frac{4}{r}\]
\[ \Rightarrow r = 2 cm\]
Now volume of the smaller cone = \[\frac{1}{3}\pi \left( CD \right)^2 \times OC = \frac{1}{3}\pi \left( 2 \right)^2 \times \frac{H}{2} = \frac{2\pi H}{3} cm\]
Height of the frustum of the cone = \[\frac{H}{2}\]
Volume of frustum of cone = \[\frac{1}{3}\pi h\left[ r_1^2 + r_1 r_2 + r_2^2 \right]\]
\[= \frac{1}{3}\pi\left( \frac{H}{2} \right)\left[ \left( 4 \right)^2 + \left( 2 \right)^2 + 4 \times 2 \right]\]
\[ = \frac{14\pi H}{3} {cm}^3\]
\[\frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{\frac{2\pi H}{3}}{\frac{14\pi H}{3}}\]
\[ \Rightarrow \frac{\text { Volume of the smaller cone }}{\text { Volume of the frustum of the cone }} = \frac{1}{7}\]
Hence, the ratio of the volumes of the two parts will be 1 : 7.
APPEARS IN
संबंधित प्रश्न
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water . The radii of the top and bottom are 28 cm and 21 cm respectively . Find the height of the bucket .
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the value of the cylinder to that of the cone.
The height and radius of the cone of which the frustum is a part are h1 and r1 respectively. If h2 and r2 are the heights and radius of the smaller base of the frustum respectively and h2 : h1 = 1 : 2, then r2 : r1 is equal to
A fez, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, radius at the upper base is
4 cm and its slant height is 15 cm, then find the area of material used for making it.
The slant height of the frustum of a cone having radii of two ends as 5 cm and 2 cm respectively and height 4 cm is ______.
The volume of the frustum of a cone is `1/3 pih[r_1^2 + r_2^2 - r_1r_2]`, where h is vertical height of the frustum and r1, r2 are the radii of the ends.
