Advertisements
Advertisements
प्रश्न
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
उत्तर
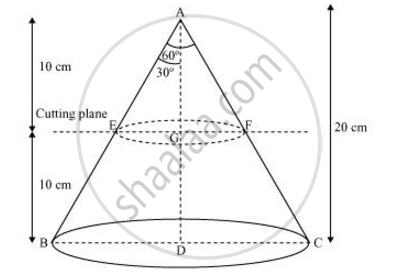
In ΔAEG,
EG/AG = tan 30º
`EG = 10/sqrt3 cm = (10sqrt3)/3`
In ΔABD,
BD/AD = tan 30º
`BD = 20/sqrt3 = (20sqrt3)/3cm`
Radius (r1) of upper end of frustum = `(10sqrt3)/3 cm`
Radius (r2) of lower end of container = `(20sqrt3)/3cm `
Height (h) of container = 10 cm
Volume of frustum = `1/3pih(r_1^2+r_2^2+r_1r_2)`
`=1/3xxpixx10[((10sqrt3)/3)^2 + ((20sqrt3)/3)^2 + ((10sqrt3)(10sqrt3))/(3xx3)]`
`= 10/3pi[100/3+400/3+200/3]`
`=10/3xx22/7xx700/3=22000/9 cm^3`
Radius (r) of wire = = `1/16xx1/2 = 1/32cm`
Let the length of wire be l.
Volume of wire = Area of cross-section × Length
= (πr2) (l)
=pi(1/32)^2 xx l
Volume of frustum = Volume of wire
`22000/9 = 22/7xx(1/32)^2xxl`
`7000/9 xx1024 = l`
l = 796444.44 cm
= 7964.44 meters
APPEARS IN
संबंधित प्रश्न
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
Derive the formula for the curved surface area and total surface area of the frustum of cone.
A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the cone and of the remaining solid left out after the cone carved out.
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces?
A reservoir is in the shape of a frustum of a right circular cone. It is 8 m across at the top and 4 m across at the bottom. If it is 6 m deep, then its capacity is
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.