Advertisements
Advertisements
Question
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
Solution
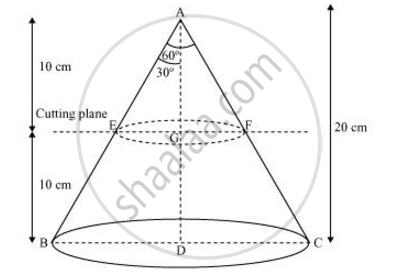
In ΔAEG,
EG/AG = tan 30º
`EG = 10/sqrt3 cm = (10sqrt3)/3`
In ΔABD,
BD/AD = tan 30º
`BD = 20/sqrt3 = (20sqrt3)/3cm`
Radius (r1) of upper end of frustum = `(10sqrt3)/3 cm`
Radius (r2) of lower end of container = `(20sqrt3)/3cm `
Height (h) of container = 10 cm
Volume of frustum = `1/3pih(r_1^2+r_2^2+r_1r_2)`
`=1/3xxpixx10[((10sqrt3)/3)^2 + ((20sqrt3)/3)^2 + ((10sqrt3)(10sqrt3))/(3xx3)]`
`= 10/3pi[100/3+400/3+200/3]`
`=10/3xx22/7xx700/3=22000/9 cm^3`
Radius (r) of wire = = `1/16xx1/2 = 1/32cm`
Let the length of wire be l.
Volume of wire = Area of cross-section × Length
= (πr2) (l)
=pi(1/32)^2 xx l
Volume of frustum = Volume of wire
`22000/9 = 22/7xx(1/32)^2xxl`
`7000/9 xx1024 = l`
l = 796444.44 cm
= 7964.44 meters
APPEARS IN
RELATED QUESTIONS
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom . Find the volume of water left in the cylinder , if the radius of the cylinder is equal to the radius of te cone
If a cone and a sphere have equal radii and equal volumes. What is the ratio of the diameter of the sphere to the height of the cone?
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
A container, open at the top and made up of metal sheet, is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm, respectively. Find the cost of metal sheet used to make the container, if it costs ₹10 per 100 cm2
Choose the correct answer of the following question:
If the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm, then its slant height is
A cone is cut through a plane parallel to its base and then the cone that is formedon one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
The slant height of the frustum of a cone having radii of two ends as 5 cm and 2 cm respectively and height 4 cm is ______.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
The curved surface area of a frustum of a cone is πl (r1 + r2), where `l = sqrt(h^2 + (r_1 + r_2)^2)`, r1 and r2 are the radii of the two ends of the frustum and h is the vertical height.
