Advertisements
Advertisements
Question
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
Solution
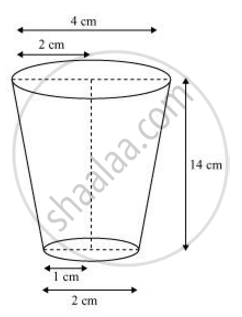
Radius (r1) of upper base of glass = 4/2 = 2 cm
Radius (r2) of lower base of glass = 2/2 = 1 cm
Capacity of glass = Volume of frustum of cone
`= 1/3pih = (r_1^2+r_2^2+r_1r_2)`
`=1/3pih[(2)^2 +(1)^2+(2)(1)]`
`=1/3xx22/7xx14[4+1+2]`
= 308/3 = 102 2/3 cm3
Therefore, the capacity of the glass is 102 2/3 cm3
RELATED QUESTIONS
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its total surface area.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 16 cm and 12 cm. Find the capacity of the glass.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, then find the height of the bucket.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m, respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal.)
