Advertisements
Advertisements
Question
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
Solution
Here, r1 = 14 cm, r2 = 6 cm and h = 6 cm.
Slant height of the frustum, l = \[\sqrt{h^2 + \left( r_2 - r_1 \right)^2} = \sqrt{6^2 + \left( 14 - 6 \right)^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100}\]= 10 cm
Volume of the frustum
\[= \frac{1}{3}\pi h\left( r_1^2 + r_1 r_2 + r_2^2 \right)\]
\[ = \frac{1}{3} \times 3 . 14 \times 6 \times \left( {14}^2 + 14 \times 6 + 6^2 \right)\]
\[ = 3 . 14 \times 2 \times \left( 196 + 84 + 36 \right)\]
\[ = 6 . 28 \times 316\]
\[ = 1984 . 48 {cm}^3\]
RELATED QUESTIONS
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm2. [Take π = 3.14]
A metallic solid sphere of radius 10.5 cm is melted and recasted into smaller solid cones, each of radius 3.5 cm and height 3 cm. How many cones will be made?
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is `1/27` of the given cone, then at what height it is cut from its base?
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
If the areas of circular bases of a frustum of a cone are 4 cm2 and 9 cm2 respectively and the height of the frustum is 12 cm. What is the volume of the frustum?
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular is
A cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
The maximum volume of a cone that can be carved out of a solid hemisphere of radius r is
The radii of the circular ends of a frustum are 6 cm and 14 cm. If its slant height is 10 cm, then its vertical height is
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
A container in the shape of a frustum of a cone having diameters of its two circular faces as 35 cm and 30 cm and vertical height 14 cm,
is completely filled with oil. If each cm3 of oil has mass 1.2 g, then find the cost of oil in the container if it costs ₹40 per kg.
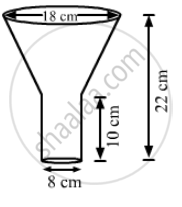
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
The number of conical bottles of radius 2 cm and height 3.6 cm, required to empty the liquid from a cylindrical bottle of radius 6 cm and height 10 cm is ______.
The slant height of the frustum of a cone having radii of two ends as 5 cm and 2 cm respectively and height 4 cm is ______.
A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 22 per litre which the container can hold.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
