Advertisements
Advertisements
Question
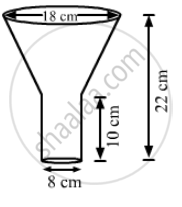
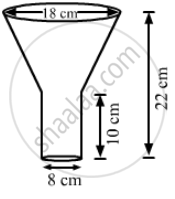
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
Solution
We have,
Height of the cylindrical portion, h = 10 cm,
height of the frustum of cone portion, H = 22 - 10 = 12 cm,
Radius of the cylindrical portion = Radius of smaller end of frustum portion,
Radius of larger end of frustum portion, R = 18/2 = 9 cm
Also, the slant height of the frustum, `l = sqrt(("R - r")^2 + "H"^2)`
`=sqrt((9 - 4)^2+12^2`
`=sqrt(5^2+12^2)`
`=sqrt(25+144`
`=sqrt(169)`
`=13 "cm"`
Now,
The area of the tin sheet required = CSA of frustum of cone + CSAA of cylinder
= π (R + r) l + 2πrh
`= 22/7xx(9+4)x13+2xx22/7xx4xx10`
`=22/7xx13xx13+22/7xx80`
`= 22/7xx(169+80)`
`=22/7xx249`
≈ 782.57 cm2
So, the area of the tin sheet required to make the funnel is 782.57 cm2.
APPEARS IN
RELATED QUESTIONS
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
Derive the formula for the curved surface area and total surface area of the frustum of cone.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2, then write the ratio of the height of the cone of which the frustum is a part to the height fo the frustum.
A bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm, respectively. Find how many litres of water can the bucket hold.
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of ₹30 per litre, which the bucket can hold.
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is `"10459" 3/7 "cm"`. The radii of its lower and upper circular ends are 8 cm and 20 cm, respectively. Find the cost of metal sheet used in making the container at the rate of ₹1.40 per cm2.
A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹ 22 per litre which the container can hold.
