Advertisements
Advertisements
Question
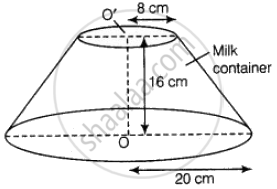
A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹ 22 per litre which the container can hold.
Solution
Given that, height of milk container (h) = 16 cm,
Radius of lower end of milk container (r) = 8 cm
And radius of upper end of milk container (R) = 20 cm
∴ Volume of the milk container made of metal sheet in the form of a frustum of a cone
= `(πh)/3 (R^2 + r^2 + Rr)`
= `22/7 xx 16/3 [(20)^2 + (8)^2 + 20 xx 8]`
= `(22 xx 16)/21 (400 + 64 + 160)`
= `(22 xx 16 xx 624)/21`
= `219648/21`
= 10459.42 cm3 ......[∵ 1L = 1000 cm3]
= 10.45942 L
So, volume of the milk container is 10459.42 cm3
∵ Cost of 1 L milk = ₹ 22
∴ Cost of 10.45942 L milk = 22 × 10.45942 = ₹ 230.12
Hence, the required cost of milk is ₹ 230.12
APPEARS IN
RELATED QUESTIONS
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the cost of milk at the rate of ₹44 per litre which the container can hold.
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water . The radii of the top and bottom are 28 cm and 21 cm respectively . Find the height of the bucket .
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side of 3 cm to form a cone. The volume of the cone so formed is
The diameters of the ends of a frustum of a cone are 32 cm and 20 cm. If its slant height is 10 cm, then its lateral surface area is
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, then find the height of the bucket.
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are
20 cm and 12 cm, respectively. Find the height of the bucket. [Use π = 3.14]
A milk container is made of metal sheet in the shape of frustum of a cone whose volume is `"10459" 3/7 "cm"`. The radii of its lower and upper circular ends are 8 cm and 20 cm, respectively. Find the cost of metal sheet used in making the container at the rate of ₹1.40 per cm2.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter `"4"2/3` cm and height 3 cm. Find the number of cones so formed.
A funnel is a combination of
The number of conical bottles of radius 2 cm and height 3.6 cm, required to empty the liquid from a cylindrical bottle of radius 6 cm and height 10 cm is ______.
The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of the bucket is ______.
The curved surface area of a frustum of a cone is πl (r1 + r2), where `l = sqrt(h^2 + (r_1 + r_2)^2)`, r1 and r2 are the radii of the two ends of the frustum and h is the vertical height.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
