Advertisements
Advertisements
Question
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter `"4"2/3` cm and height 3 cm. Find the number of cones so formed.
Solution
We have,
Radius of the metallic sphere, R `= 28/2 = 14 "cm"`
Radius of the smaller cone, t `= "r" =1/2xx("4"2/3)=1/2xx14/3xx7/3 "cm"`
Now,
The number of cones so formed `= "Volume of the metallic sphere"/"Volume of a smaller cone"`
`=((4/3pi"R"^3))/((1/3pi"r"^2"h"))`
`="4R"^3/("r"^2"h")`
`=(4xx14xx14xx14)/(7/3xx7/3xx3)`
= 672
So, the number of cones so formed is 672.
Disclaimer: The answer given in the textbook is incorrect. The same has been corrected above.
APPEARS IN
RELATED QUESTIONS
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
If a cone and a sphere have equal radii and equal volumes. What is the ratio of the diameter of the sphere to the height of the cone?
A solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h. If the total volume of the solid is 3 times the volume of the cone, then the height of the circular is
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. Find the radius of the base of the cone.
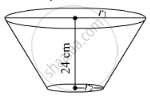
A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of ₹30 per litre, which the bucket can hold.
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

A cone is cut through a plane parallel to its base and then the cone that is formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called ______.
An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 22 per litre which the container can hold.
