Advertisements
Advertisements
प्रश्न
A milk container of height 16 cm is made of metal sheet in the form of frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹ 22 per litre which the container can hold.
उत्तर
Given that, height of milk container (h) = 16 cm,
Radius of lower end of milk container (r) = 8 cm
And radius of upper end of milk container (R) = 20 cm
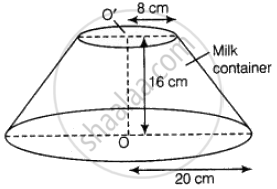
∴ Volume of the milk container made of metal sheet in the form of a frustum of a cone
= `(πh)/3 (R^2 + r^2 + Rr)`
= `22/7 xx 16/3 [(20)^2 + (8)^2 + 20 xx 8]`
= `(22 xx 16)/21 (400 + 64 + 160)`
= `(22 xx 16 xx 624)/21`
= `219648/21`
= 10459.42 cm3 ......[∵ 1L = 1000 cm3]
= 10.45942 L
So, volume of the milk container is 10459.42 cm3
∵ Cost of 1 L milk = ₹ 22
∴ Cost of 10.45942 L milk = 22 × 10.45942 = ₹ 230.12
Hence, the required cost of milk is ₹ 230.12
APPEARS IN
संबंधित प्रश्न
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is `1/27` of the given cone, then at what height it is cut from its base?
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its total surface area.
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A cone of height 20 cm and radius of base 5 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
The radii of the base of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes?
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces?
A metallic sphere of radius 10.5 cm is melted and then recast into small cones, each of radius 3.5 cm and height 3 cm. The number of such cones is
The radii of the circular ends of a frustum are 6 cm and 14 cm. If its slant height is 10 cm, then its vertical height is
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A tent is made in the form of a frustum of a cone surmounted by another cone. The diameters of the base and the top of the frustum are 20 m and 6 m, respectively, and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, find the quantity of canvas required.
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter `1/12` cm, then find the length of the wire.
A fez, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, radius at the upper base is
4 cm and its slant height is 15 cm, then find the area of material used for making it.
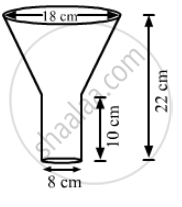
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
A shuttlecock used for playing badminton has the shape of the combination of ______.
