Advertisements
Advertisements
प्रश्न
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
उत्तर
Given,
Radius of the hemisphere = Radius of the cone.
Now,
Volume of the hemisphere `2/3 piR^3`
and
Volume of the cone `1/3 piR^2 H`
Volume of the hemisphere = volume of the cone
`2/3 piR^2 = 1/3 piR^2 H`
`2R = H` or `H/R = 2`
APPEARS IN
संबंधित प्रश्न
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its volume \[\pi\] = 3.14)
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
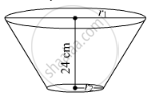
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the cost of milk at the rate of ₹44 per litre which the container can hold.
A rectangular vessel of dimensions 20 cm × 16 cm × 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).
If the areas of circular bases of a frustum of a cone are 4 cm2 and 9 cm2 respectively and the height of the frustum is 12 cm. What is the volume of the frustum?
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.
If radius of the base of cone is 7 cm and height is 24 cm, then find its slant height.
