Question

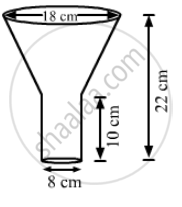
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required.(Use π = 22/7).

Answer 1

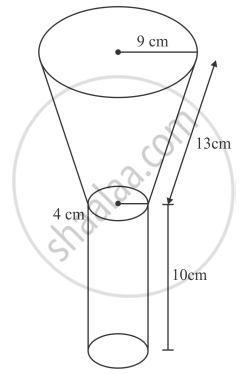
Let r₁ and r₂ (r₁ > r₂) be the radii of the ends of the frustum of a cone. Suppose l and hbe the slant height and height of frustum of cone.

Diameter of top of the frustum `2r_1 = 18 cm`

                                                   `r_1 = 9 cm`                         

Diameter of top of frustum `2r_2 = 8 cm`

                                              `r_2 = 4 cm`

Let h₁ be the height of the cylindrical portion.
Now, h₁ = 10 cm
Total height of the funnel = 22 cm
height of frustum of cone, h = 22−10 = 12 cm

\[l = \sqrt{\left( r_1 - r_2 \right)^2 + h^2}\]

\[ \Rightarrow l = \sqrt{\left( 9 - 4 \right)^2 + \left( 12 \right)^2}\]

\[ \Rightarrow l = \sqrt{25 + 144}\]

\[ \Rightarrow l = \sqrt{169}\]

\[ \Rightarrow l = 13 cm\]

Curved surface area of funnel = CSA of frustum of cone + CSA of cylinder

Curved surface area of funnel = \[\pi\left( r_1 + r_2 \right)l + 2\pi r_2 h_1\]

Therefore,

Area of the tin required

\[= \pi\left( r_1 + r_2 \right)l + 2\pi r_2 h_1 \]

\[ = \pi\left[ \left( r_1 + r_2 \right)l + 2 r_2 h_1 \right]\]

\[ = \pi\left[ \left( 9 + 4 \right) \times 13 + 2 \times 4 \times 10 \right]\]

\[ = \pi\left[ 169 + 80 \right]\]

\[ = \pi\left[ 249 \right]\]

\[ = 249\pi {cm}^2\]