Advertisements
Advertisements
प्रश्न
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
उत्तर
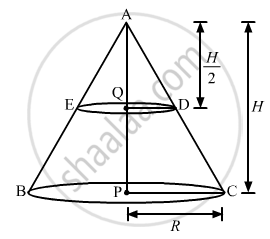
Consider a cone of radius R and height H.
Let a cone of height `H/2` is cutout from this cone whose base is parallel to the original cone. Now is
`Delta AQD and Delta APC, QD || PC`
`Delta AQD ∼ Delta APC`
`(QD)/(PC) = (AQ)/(AP)`
`QD/2 = H/(2/H)`
`QD = R/2`
Volume of cone ABC `=1/3 pi R^2 H`
Volume of cone ADE
`=1/3 pi (R/2)^2 (H/2)`
`=1/8[1/3 piR^2H]`
`=1/8`volume of cone ABC
Now volume of remaining frustum of cons EDCB
= volume of cone ABC − volume of cone AED
\[= \frac{7}{8}(\text { volume of cone ABC})\]
Comparing the volume of cone AED and frustum EDBC we get, the ratio 1 : 7.
APPEARS IN
संबंधित प्रश्न
Derive the formula for the volume of the frustum of a cone.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom . Find the volume of water left in the cylinder , if the radius of the cylinder is equal to the radius of te cone
A bucket, made of metal sheet, is in the form of a cone whose height is 35 cm and radii of circular ends are 30 cm and 12 cm. How many litres of milk it contains if it is full to the brim? If the milk is sold at Rs 40 per litre, find the amount received by the person.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water . The radii of the top and bottom are 28 cm and 21 cm respectively . Find the height of the bucket .
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 16 cm and 12 cm. Find the capacity of the glass.
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
The radii of the top and bottom of a bucket of slant height 13 cm are 9 cm and 4 cm respectively. The height of the bucket is ______.
