Question

If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is

विकल्प

• 1 : 2

• 1: 4

•  1 : 6

• 1 : 8

Answer 1

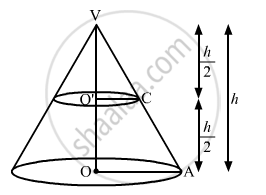
Since,

 `Delta VOA ∼ Delta VO'C`

Therefore,

In `Delta VOA ` and  `Delta VO'C`

\[\frac{O'V}{OV} = \frac{O'C}{OA}\]

     `(h/2)/h = (O'C)/(OA)`

      `1/2 =(O'C)/(OA)`

`(O'C)/(OA) = 1/2`

The ratio of the volume of upper part and the cone,

`V_1/V_2 = (1/3pi(O'C) xx h/2)/ (1/3pi(OA)^2 xx h)`

`V_1/V_2 = ((O'C)/(OA))^2 xx 1/2                      ........... (2)`

From eq. (1) and (2),

We get,

`V_1/V_2 = (1/2)^2 xx 1/2`

`V_1/V_2 = 1/4 xx 1/2`

`V_1 : V_2 = 1 : 8`