Question

The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \[\frac{1}{27}\] of the volume of the given cone, then the height above the base at which the section has been made, is

विकल्प

• 10 cm

• 15 cm

• 20 cm

• 25 cm

Answer 1

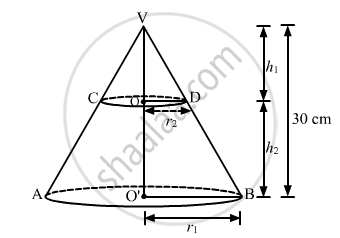
Let VAB be cone of height 30 cm and base radius r₁ cm.

Suppose it is cut off by a plane parallel to the base at a height h₂ from the base of the cone.

Clearly 

\[∆ VOD~ ∆ VO'B\]

Therefore,

\[\frac{OV}{O'V} = \frac{OD}{O'B}\]

\[ \Rightarrow \frac{h_1}{30} = \frac{r_2}{r_1}\]

But,

\[\text { Volume of cone VCD}  = \frac{1}{27}\text { Volume of cone VAB }\]

\[ \Rightarrow \frac{1}{3}\pi \left( r_2 \right)^2 h_1 = \frac{1}{27}\left( \frac{1}{3}\pi \left( r_1 \right)^2 30 \right)\]

\[ \Rightarrow \left( \frac{r_2}{r_1} \right)^2 h_1 = \frac{10}{9}\]

\[ \Rightarrow \left( \frac{h_1}{30} \right)^2 h_1 = \frac{10}{9}\]

\[ \Rightarrow h_1 = 10\]

Hence,

Required height 

= 30 -10

= 20 cm