Advertisements
Advertisements
प्रश्न
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \[\frac{1}{27}\] of the volume of the given cone, then the height above the base at which the section has been made, is
पर्याय
10 cm
15 cm
20 cm
25 cm
उत्तर
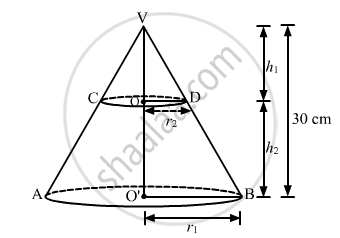
Let VAB be cone of height 30 cm and base radius r1 cm.
Suppose it is cut off by a plane parallel to the base at a height h2 from the base of the cone.
Clearly
\[∆ VOD~ ∆ VO'B\]
Therefore,
\[\frac{OV}{O'V} = \frac{OD}{O'B}\]
\[ \Rightarrow \frac{h_1}{30} = \frac{r_2}{r_1}\]
But,
\[\text { Volume of cone VCD} = \frac{1}{27}\text { Volume of cone VAB }\]
\[ \Rightarrow \frac{1}{3}\pi \left( r_2 \right)^2 h_1 = \frac{1}{27}\left( \frac{1}{3}\pi \left( r_1 \right)^2 30 \right)\]
\[ \Rightarrow \left( \frac{r_2}{r_1} \right)^2 h_1 = \frac{10}{9}\]
\[ \Rightarrow \left( \frac{h_1}{30} \right)^2 h_1 = \frac{10}{9}\]
\[ \Rightarrow h_1 = 10\]
Hence,
Required height
= 30 -10
= 20 cm
APPEARS IN
संबंधित प्रश्न
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is `14/3` m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct upto one place of decimal?
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
A cylindrical vessel of radius 4 cm contains water. A solid sphere of radius 3 cm is lowered into the water until it is completely immersed. The water level in the vessel will rise by
A farmer connects a pipe of internal diameter 25 cm from a canal into a cylindrical tank in his field, which is 12 m in diameter and 2.5 m deep. If water flows through the pipe at the rate of 3.6 km/hr, then in how much time will the tank be filled? Also, find the cost of water if the canal department charges at the rate of ₹ 0.07 per m3.
If the surface area of a sphere is 616 cm2, its diameter (in cm) is ______. (Taking π = `22/7`)
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
