Advertisements
Advertisements
प्रश्न
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
उत्तर
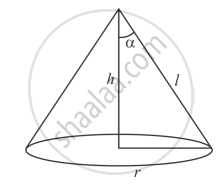
\[\sin \alpha = \frac{r}{l}\]
\[ \Rightarrow r \cos ec \ \alpha = l\]
\[\tan \alpha = \frac{r}{h}\]
\[ \Rightarrow\text { r cot } \alpha = h\]
`"volume = 1/3 pir^2h"`
`=1/3 pir^2 . r cost \ alpha`
`=1/3 pir^2 cot \ alpha`
Surface area = `pirl`
= πr2 cosec α.
= πr2 cosec α.
APPEARS IN
संबंधित प्रश्न
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass approximately. (Use : π = 355/115)
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube?
πThe height of a cylinder is 14 cm and its curved surface area is 264 cm2. The volume of the cylinder is
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, then find the total area of the canvas required.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.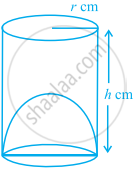
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
A bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
