Advertisements
Advertisements
Question
The radius of the base of a right circular cone of semi-vertical angle α is r. Show that its volume is \[\frac{1}{3} \pi r^3\] cot α and curved surface area is πr2 cosec α.
Solution
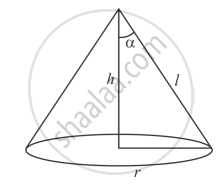
\[\sin \alpha = \frac{r}{l}\]
\[ \Rightarrow r \cos ec \ \alpha = l\]
\[\tan \alpha = \frac{r}{h}\]
\[ \Rightarrow\text { r cot } \alpha = h\]
`"volume = 1/3 pir^2h"`
`=1/3 pir^2 . r cost \ alpha`
`=1/3 pir^2 cot \ alpha`
Surface area = `pirl`
= πr2 cosec α.
= πr2 cosec α.
APPEARS IN
RELATED QUESTIONS
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5m and height 21m and the cone has a slant height 8m. Calculate total surface area and volume of the rocket?
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of wood in the toy. `[\text{Use}pi 22/7]`
Find the surface area of a sphere of radius 7 cm.
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4, what is the ratio of their volumes?
The volume of a sphere is 4851 cm3. Find its curved surface area.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
The total surface area of a hemisphere of radius 7 cm is
Arrange the given objects according to their volume
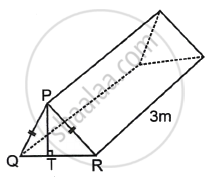
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent