Advertisements
Advertisements
Question
Find the surface area of a sphere of radius 7 cm.
Solution
Given: Radius of the sphere, r = 7 cm
∴ Surface area of the sphere, S = `4pir^2`
`= 4 xx 22/7 xx (7)^2`
`= 4 xx 22/7 xx 49`
= 88 × 7
= 616 cm2
Thus, the surface area of sphere is 616 cm2.
RELATED QUESTIONS
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3 `5/9` cm. Find the diameter of the cylindrical vessel.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is `14/3` m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
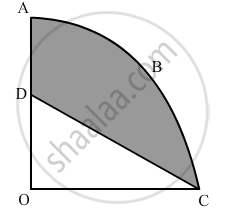
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A hemispherical bowl of internal radius 9 cm is full of water. Its contents are emptied in a cylindrical vessel of internal radius 6 cm. Find the height of water in the cylindrical vessel.
Find the ratio of the volumes of a cylinder and a cone having equal radius and equal height.
(A)1 : 2 (B) 2 : 1 (C) 1 : 3 (D) 3 : 1
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1m3 of metal weighs 21g.
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs 45 per m2.
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and the slant height of the conical portion is 53 m, find the area of canvas needed to make the tent.
The rain water from a roof of 44 m × 20 m drains into a cylindrical tank having diameter of base 4 m and height 3.5 m. If the tank is just full, then find the rainfall in cm.
66 cubic cm of silver is drawn into a wire 1 mm in diameter. Calculate the length of the wire in metres.
The radius of the base of a cone is 5 cm and its height is 12 cm. Its curved surface area is
Assertion (A)
The curved surface area of a cone of base radius 3 cm and height 4 cm is 15π cm2.\
Reason (R)
Volume of a cone = πr2h
- Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
- Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
- Assertion (A) is true and Reason (R) is false.
- Assertion (A) is false and Reason (R) is true.
The dimensions of a metallic cuboid are 44 cm × 42 cm × 21 cm. it is molten and recast into a sphere. Find the surface area of the sphere.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is ______.
Find the surface area of a sphere of radius 7 cm.
Solution :
The surface area of the sphere = 4πr2
= `4 xx 22/7 xx square^2`
= `4 xx 22/7 xx square`
= `square xx 7`
∴ The surface area of the sphere = `square` sq.cm.
