Advertisements
Advertisements
Question
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is ______.
Options
192
384
480
2592
Solution
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is 192.
Explanation:
Since, the solid has rectangular faces.
So, we have `l xx b = 16` ...(i)
`b xx h = 32` ...(ii)
`l xx h = 72` ...(iii)
Where `l, b` and `h` are the length, breadth and height respectively, of the solid.
On multiplying equations (i), (ii) and (iii), we get
`l xx b xx b xx h xx l xx h = 16 xx 32 xx 72`
⇒ `l^2 xx b^2 xx h^2 = 36864`
⇒ `(lbh)^2 = 36864`
∴ `lbh = 192`
Hence, the volume of the solid is 192 cu cm.
APPEARS IN
RELATED QUESTIONS
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water.The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. (Use 𝜋 = 3.14).
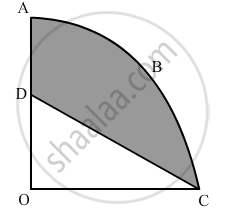
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
A sphere of maximum volume is cut-out from a solid hemisphere of radius r, what is the ratio of the volume of the hemisphere to that of the cut-out sphere?
The diameters of two circular ends of the bucket are 44 cm and 24 cm . The height of the bucket is 35 cm . The capacity of the bucket is
The surface area of a sphere is 2464 cm2. If its radius be doubled, then what will be the surface area of the new sphere?
A spherical ball of diameter 21 cm is melted and recast into cubes, each of side 1 cm. Find the number of cubes so formed.
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
A shuttlecock used for playing badminton is a combination of

The slant height of a bucket is 45 cm and the radii of its top and bottom are 28 cm and 7 cm, respectively. The curved surface area of the bucket is
