Advertisements
Advertisements
Question
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100 cm2. [Use π = 3.14]
Solution
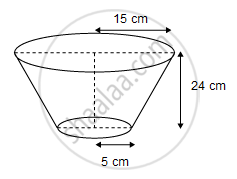
Diameter of upper end of bucket = 30 cm
∴ Radius (r1) of upper end of bucket = 15 cm
Diameter of lower end of bucket = 10 cm
∴ Radius (r2) of lower end of bucket = 5 cm
Height (h) of bucket = 24 cm
Slant height (l) of frustum =`sqrt((r_1-r_2)^2+h^2)`
`=sqrt((15-5)^2+(24)^2)=sqrt((10)^2+(24)^2)=sqrt(100+576)`
`=sqrt676=26`cm
Area of metal sheet used to make the bucket `pi(r_1+r_2)l+pir_2^2` = π (15 + 5) 26 + π (5)2 = 520 π + 25 π = 545 π cm2
Cost of 100 cm2 metal sheet = Rs 10
Cost of 545`pi cm^2`metal sheet = Rs `(545xx3.14xx10)/100=Rs 171.13`
Therefore, cost of metal sheet used to make the bucket is Rs 171.13.
APPEARS IN
RELATED QUESTIONS
A metal parallelopiped of measures 16 cm x 11 cm x 10 cm was melted to make coins. How many coins were made if the thickness and diameter of each coin were 2 mm and 2 cm respectively?
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
A wall 24 m , 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm \[\times\] 16 cm \[\times\] 10 cm . If the mortar occupies \[\frac{1}{10}th\] of the volume of the wall, then find the number of bricks used in constructing the wall.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, then find its capacity and total surface area.
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. The height of the pillar is
The ratio between the volume of two spheres is 8 : 27. What is the ratio between their surface areas?
The diameter of a sphere is 42 cm. It is melted and drawn into a cylindrical wire of diameter 2.8 cm. Find the length of the wire.
If the side of a cube is 5 cm, then find its volume.
The volume of a sphere is 4851 cm3. Its diameter is ______.
