Advertisements
Advertisements
Question
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

Solution
The remaining solid is a frustum of the given cone
Total surface area of the frustum = πl(r1+r2)+πr12+πr22
Where
h = Height of the frustum = 12−4 = 8 cm
r1 = Larger radius of the frustum = 6 cm
r2 = Smaller radius of the frustum
l = Slant height of the frustum
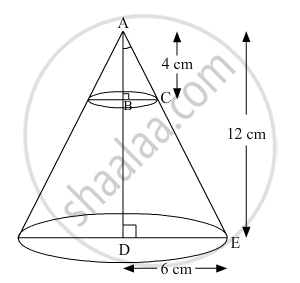
In the given figure, ∆ABC ~ ∆ADE by AA similarity criterion.
`:.(BC)/(DC)=(AB)/(AD)`
`=>r_2/6=4/12`
⇒r2=2 cm
We know
`l = sqrt(h^2+(r_1-r_2)^2)`
`=>l=sqrt(8^2+(6-1)^2)`
`=>l = 4sqrt5 `
∴ Total surface area of the frustum = πl(r1+r2)+πr12+πr22
= π×4`sqrt5`(6+2)+π×62+π×22
`=pi(32sqrt5+40)`
`=22/7xx111.552`
= 350.592 cm2
Hence, the total surface area of the remaining solid is 350.592 cm2.
APPEARS IN
RELATED QUESTIONS
The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find:
1) The area of the metal sheet used to make the bucket.
2) Why we should avoid the bucket made by ordinary plastic? [Use π = 3.14]
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m , the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
A bucket made of aluminum sheet is of height 20cm and its upper and lower ends are of radius 25cm an 10cm, find cost of making bucket if the aluminum sheet costs Rs 70 per
100 cm2
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. [User `pi22/7`]
A solid sphere of radius 'r' is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thickness 2 cm, find the value of 'r'.
A solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is
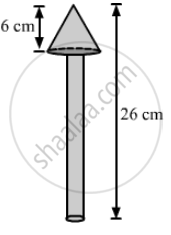
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure. The total height of the toy is 26 cm, while the height of the conical part is 6 cm. The diameter of the base of the conical part is 5 cm and that of the cylindrical part is 4 cm. The conical part and the cylindrical part are respectively painted red and white. Find the area to be painted by each of these colours. `["Take" pi = 22/7]`
Find the ratio of the volume of a cube to that of a sphere which will fit inside it.
A plumbline (sahul) is a combination of
Statement A (Assertion): Total Surface area of the top is the sum of the curved surface area of the hemisphere and the curved surface area of the cone.
Statement R( Reason): Top is obtained by joining the plane surfaces of the hemisphere and cone together.

