Advertisements
Advertisements
प्रश्न
In Fig. 4, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use `pi=22/7` and `sqrt5=2.236`)

उत्तर
The remaining solid is a frustum of the given cone
Total surface area of the frustum = πl(r1+r2)+πr12+πr22
Where
h = Height of the frustum = 12−4 = 8 cm
r1 = Larger radius of the frustum = 6 cm
r2 = Smaller radius of the frustum
l = Slant height of the frustum
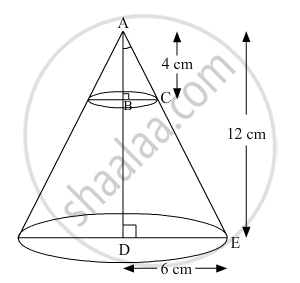
In the given figure, ∆ABC ~ ∆ADE by AA similarity criterion.
`:.(BC)/(DC)=(AB)/(AD)`
`=>r_2/6=4/12`
⇒r2=2 cm
We know
`l = sqrt(h^2+(r_1-r_2)^2)`
`=>l=sqrt(8^2+(6-1)^2)`
`=>l = 4sqrt5 `
∴ Total surface area of the frustum = πl(r1+r2)+πr12+πr22
= π×4`sqrt5`(6+2)+π×62+π×22
`=pi(32sqrt5+40)`
`=22/7xx111.552`
= 350.592 cm2
Hence, the total surface area of the remaining solid is 350.592 cm2.
APPEARS IN
संबंधित प्रश्न
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
The number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm, is:
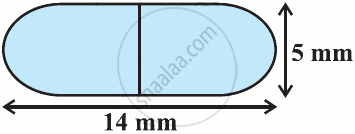
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2
[use `pi = 22/7`]
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid.
If the total surface area of a solid hemisphere is 462 cm2, then find its volume.
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, are melted and recast into a single large cube. Find the edge of the new cube formed.
In a right circular cone, the cross-section made by a plane parallel to the base is a
