Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
Notes
We have already learnt about the surface area and volumes of figures, but in this chapter we will given different combinations of solids. We are known with solids like cylinder, sphere, cone, cuboid, rectangle, square, etc. In this chapter we are suppose to find surface areas of different combinations of solids.
Now before we proceed, we must understand what is curved surface area. The solids having curved surface are cone, cylinder. Curved surface area is the outer portion, the area of flat ends of such solids will not be included while calculating Curved surface area. But while calculating Total surface area we must include the area of flat ends of the solids, provided that the solid should not be hollow from inside.
Example- 2 cubes each of volume `64 cm^3` are joined end to end. Find the surface area of the resulting cuboid.
Solution- `Volume of cube= 64cm^3`
`"edge"^3= 64cm^3`
`"edge of cube"` = `3 sqrt 64` cm
edge= 4 cm
By adding this two cube we get a cuboid
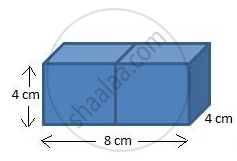
So we get dimensions of cuboid as
As we have two cube the lenght will be doubled
therefore, lenght = 2(4)= 8cm
breadth= 4cm
height= 4cm
Surface area of cuboid= 2 (lb+bh+hl)
= `2 (8 xx 4)+(4 xx 4)+(4 xx 8
)`
=` 2 (32+16+32)`
= `2 (80)`
Surface area of cuboid= `160 cm^2`
Video Tutorials
Shaalaa.com | Surface Area and Volume part 2 (Surface Area)
Series: 1
00:12:18 undefined
00:11:20 undefined
00:11:09 undefined
00:10:43 undefined
00:13:38 undefined
00:05:52 undefined
00:12:20 undefined
00:09:52 undefined
