Division of a Line Segment

Construction 1 : To divide a line segment in a given ratio.

Given a line segment AB, we want to divide it in the ratio m : n, where both m and n are positive integers. To help you to understand it, we shall take m = 3 and n = 2.

Steps of Construction :

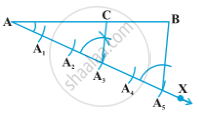
1)Draw a line AB.

2)Draw AX making an acute angle with AB.

3)Locate 5 (m + n) points `"A"_1, "A"_2, "A"_3,"A"_4 and "A"_5` on AX with the help of compass, so that `"A A"_1``= "A"_1"A"_2 = "A"_2"A"_3 = "A"_3"A"_4 = "A"_4"A"_5.`

4) Join `"BA"_5.`

5)Through the point `"A"_3` (m = 3), draw a line parallel to `"A"_5"B"` intersecting AB at the point C. Since `"A"_3"C"` is parallel to `"A"_5"B"`, therefore,

`"AA"_3/("A"_3"A"_5)= "AC"/"CB"`    (by basic proportionality theorem)

`"AA"_3/("A"_3"A"_5)= 3/2`    (by construction)

therefore, `"AC"/"CB"= 3/2`

This shows that C divides AB in the ratio 3 : 2.

Alternative Method

Steps of Construction :

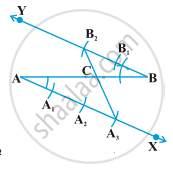
1. Draw any ray AX making an acute angle with AB.

2. Draw a ray BY || AX by making ∠ ABY equal to ∠ BAX.

3. Locate the points `"A"_1, "A"_2, "A"_3` (m = 3) on AX and `"B"_1, "B"_2`  (n = 2) on BY such that `"AA"_1` = `"A"_1"A"_2` = `"A"_2"A"_3`  = `"BB"_1` = `"B"_1"B"_2`

4. Join `"A"_3"B"_2`. Let it intersect AB at a point C

Then AC : CB = 3 : 2.

Construction 2- To construct a triangle similar to a given triangle as per given scale factor.

Example 1 : Construct a triangle similar to a given triangle ABC with its sides equal

to `3/4` of the corresponding sides of the triangle ABC.

Solution: Given a triangle ABC, we are required to construct another triangle whose

sides are `3/4` of the corresponding sides of the triangle ABC.

Steps of Construction :

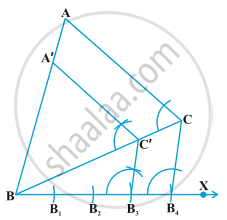
1) Draw ΔABC.

2) Draw ray BX making an acute angle with AB

3) Locate 4 equal points `"B"_1` to `"B"_4` on BX

4) Join `"B"_4"C"`

5) Draw a line through `"B"_3` || `"B"_4"C"` to intersect BC at C′

6) Draw line through C′ || AC to intersect AB at A′

Then, ∆ A′BC′ is the required triangle.

Let us now see how this construction gives the required triangle.

`"BC′"/"C′C"`  `= 3/1`   (By construction)

Therefore, `"BC"/"BC′"` `= ("BC′" + "C′ C")/"B C′"` `= 1+ "C′ C"/"B C′" ` 

`= 1+ 1/3= 4/3`

i.e `"B C′"/"BC"= 3/4`

Also C′A′ is parallel to CA. Therefore, ∆ A′BC′ ~ ∆ ABC. (Angle-Angle rule)

So, `"A′B"/"AB"= "A′C′"/"AC"= "BC′"/"BC"= 3/4`

Example 2 : Construct a triangle similar to a given triangle ABC with its sides equal

to `5/3` of the corresponding sides of the triangle ABC .

Solution : Given a triangle ABC, we are required to construct a triangle whose sides

are `5/3` of the corresponding sides of ∆ ABC.

Steps of Construction :

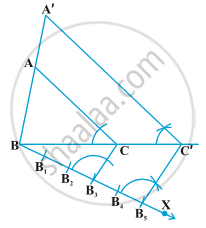
1) Draw ΔABC.

2) Draw ray BX making an acute angle with BC.

3) Locate 5 equal points `"B"_1` to `"B"_5` on BX

4) Join `"B"_3"C"`

5) Draw line through `"B"_5` parallel to `"B"_3"C"` to intersect BC at C′

6) Draw line through C′ parallel AC to intersect AB at A′

Then A′BC′ is the required triangle.

For justification of the construction, note that ∆ ABC ~ ∆ A′BC′ (Angle-Angle rule)

Therefore, `"AB"/"A′B"= "AC"/"A′C′"= "BC"/"BC′"`

But, `"BC"/"BC′"``= "BB"_3/"BB"_5= 3/5`,

so, `"BC′"/"BC"= 5/3`, and, therefore,

`"A′B"/"AB"= "A′C′"/"AC"= "BC′"/"BC"= 5/3`