Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
- Tangent theorem: A tangent at any point of a circle is perpendicular to the radius through the point of contact.
Notes
In the previous section, you have seen that a tangent to a circle is a line that intersects the circle at only one point.
1) A circle can only have one tangent at a point of the cirlce.
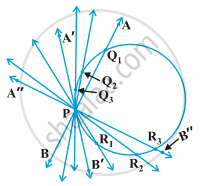
But the circle is made of infinite numbers of points therefore a circle can have infinitely many tangents. But it can only have one tangent at one point.
Theorem
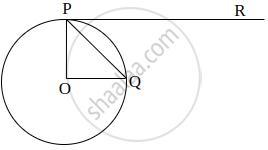
Theorem1- The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Given: A circle with centre O, a tangent XY at the point of contanct P.
To prove: OP ⊥ XY.
Construction: Take a point Q, other than P or XY. Jion OQ.
Proof: Q lies on the tangent XY.
Q lies outside the circle.
Let OQ cuts the circle at R.
OR < OQ (a part is less than a whole)
But, OR=OP (radii of the same circle)
So, OP < OQ
Thus, OP is shorter than any line segment joining O to any point on XY other than point P.
Therefore, OP is the shortest distance between O and line segment XY.
But, the shortest distance between a point and a line segment is the perpendicular distance.
Therefore, OP is perpendicular to XY.