Advertisements
Advertisements
प्रश्न
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB)=3/5`.
उत्तर
It is given that`(AP)/(AB)=3/5`.
`therefore (AP)/(PB)=(AP)/(AB-AP)=3/(5-3)=3/2`
Thus, point P divides line segment AB in the ratio 3: 2.
To draw a line segment AB of length 7 cm and mark a point P (using ruler and compass) such that `(AP)/(PB)=3/5 i,e, (AP)/(PB)=3/2`, the following steps are to be followed:
Step 1: Draw line segment AB of length 7 cm and draw a ray AX making an acute angle with line segment AB.
Step 2: Locate 5 (2 + 3) points i.e., A1, A2, A3, A4 and A5 on AX such that AA1 = A1 A2 = A2 A3 and so on.
Step 3: Join BA5.
Step 4: Through point A3 , draw a line parallel to BA5 (by making an angle equal to ∠AA5 B) at A3 intersecting AB at point P.
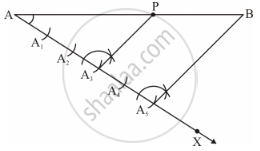
Now, P is the required point on line segment AB of length 7 cm. This point satisfies the condition`(AP)/(AB)=3/5`.
APPEARS IN
संबंधित प्रश्न
Construct the circumcircle and incircle of an equilateral triangle ABC with side 6 cm and centre O. Find the ratio of radii of circumcircle and incircle.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If \[\frac{YZ}{YQ} = \frac{6}{5},\] then construct ∆XYZ similar to ∆PYQ.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
