Advertisements
Advertisements
प्रश्न
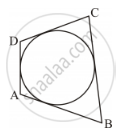
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
उत्तर
Let the inscribed circle touch sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.
It is known that the lengths of tangents drawn from an external point to a circle are equal.
∴ AS = AP, DS = DR, BP = BQ, CR = CQ
AD
= AS + DS
= AP + DR
= (6 − PB) + (8 − CR)
= 14 cm − BQ − CQ [(Using (1)]
= 14 cm − (BQ + CQ)
= 14 cm − BC
= (14 − 9) cm
= 5 cm
Thus, the length of side AD is 5 cm
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
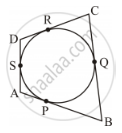
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
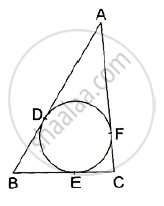
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
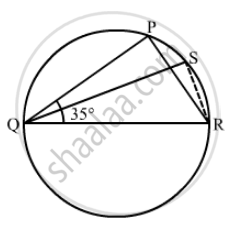
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

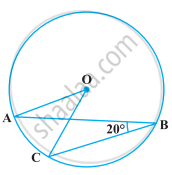
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.