Advertisements
Advertisements
Question
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
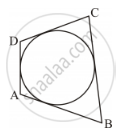
Solution
Let the inscribed circle touch sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.
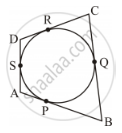
It is known that the lengths of tangents drawn from an external point to a circle are equal.
∴ AS = AP, DS = DR, BP = BQ, CR = CQ
AD
= AS + DS
= AP + DR
= (6 − PB) + (8 − CR)
= 14 cm − BQ − CQ [(Using (1)]
= 14 cm − (BQ + CQ)
= 14 cm − BC
= (14 − 9) cm
= 5 cm
Thus, the length of side AD is 5 cm
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
