Advertisements
Advertisements
Question
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
Solution
OP = 2r
Tangents drawn from external point to the circle are equal in length
PA = PB
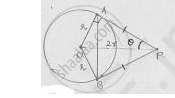
At point of contact, tangent is perpendicular to radius.
In ΔAOP, sin 𝜃 =`"opp.side"/"hypotenuse"=r/(2r)=1/2`
𝜃 = 30°
∠APB = 20 = 60°, as PA = PB ∠BAP = ∠ABP = x.
In ΔPAB, by angle sum property
∠APB + ∠BAP + ∠ABP = 180°
2x = 120° ⇒ x = 60°
In this triangle all angles are equal to 60°
∴ ΔAPB is equilateral.
APPEARS IN
RELATED QUESTIONS
Prove that the tangents at the extremities of any chord make equal angles with the chord.
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

If the radius of a circle is 5 cm, what will its diameter be?
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
