Advertisements
Advertisements
Question
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Solution
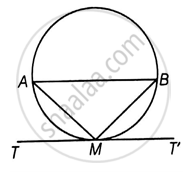
Let us draw a circle in which AMB is an arc and M is the mid-point of the arc AMB.
Joined AM and MB.
Also TT' is a tangent at point M on the circle.
To Prove: AB || TT'
Proof: As M is the mid point of Arc AMB
Arc AM = Arc MB
AM = MB ...[As equal chords cuts equal arcs]
∠ABM = ∠BAM ...[Angles opposite to equal sides are equal] [1]
Now, ∠BMT' = ∠BAM ...[Angle between tangent and the chord equals angle made by the chord in alternate segment] [2]
From [1] and [2]
∠ABM = ∠BMT'
So, AB || TT' ...[Two lines are parallel if the interior alternate angles are equal]
Hence Proved!
APPEARS IN
RELATED QUESTIONS
A circle can have ______ parallel tangents at the most.
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
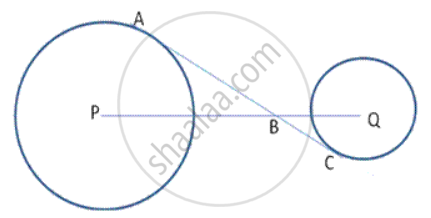
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
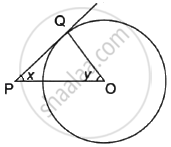
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
