Advertisements
Advertisements
Question
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Solution
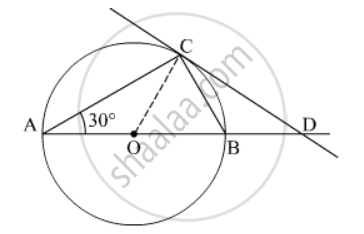
It is given that ∠BAC = 30° and AB is diameter.
∠ACB = 90° ...(Angle formed by the diameter is 90°)
In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180°
⇒ 90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
⇒ ∠CBD = 180° – 60° = 120° ...(∠CBD and ∠ABC form a linear pair)
In ∆OCD,
∠OCD = 90° ...(Angle made by Radius on the tangent)
∠OBC = ∠ABC = 60°
Since OB = OC,
∠OCB = ∠OBC = 60° ...(OC = OB = radius)
In ∆OCB,
⇒ ∠COB + ∠OCB + ∠OBC = 180°
⇒ ∠COB + 60° + 60° = 180°
⇒ ∠COB = 60°
In ∆OCD,
∠COD + ∠OCD + ∠ODC = 180°
⇒ 60° + 90° + ∠ODC = 90° ...(∠COD = ∠COB)
⇒ ∠ODC = 30°
In ∆CBD,
∠CBD = 120°
∠BDC = ∠ODC = 30°
⇒ ∠BCD + ∠BDC + ∠CBD = 180°
⇒ ∠BCD + 30° + 120° = 180°
⇒ ∠BCD + 30° = ∠BDC
Angles made by BC and BD on CD are equal, so ∆CBD is an isosceles triangle and therefore, BC = BD.
APPEARS IN
RELATED QUESTIONS
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
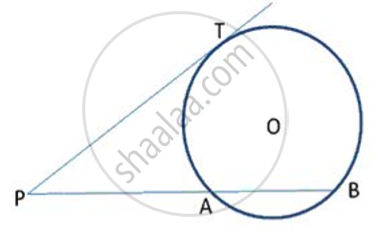
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
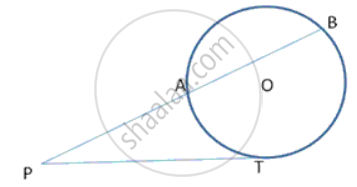
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
