Advertisements
Advertisements
Question
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
Options
Both Assertion (A) and Reason (R) are true and Reason (R) gives the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Solution
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation:
Assertion: A circle's tangent is always perpendicular to its radius through the point of contact.
Reason: Tangents drawn from an exterior point to a circle have the same length.
As a result, both reason and assertion are valid, but assertion is not the proper justification for reason.
APPEARS IN
RELATED QUESTIONS
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
How many tangents can be drawn to a circle from a point on it?
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

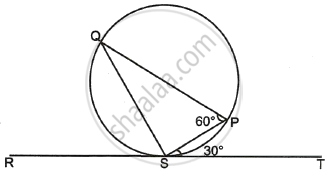
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.