Advertisements
Advertisements
प्रश्न
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
विकल्प
Both Assertion (A) and Reason (R) are true and Reason (R) gives the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
उत्तर
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation:
Assertion: A circle's tangent is always perpendicular to its radius through the point of contact.
Reason: Tangents drawn from an exterior point to a circle have the same length.
As a result, both reason and assertion are valid, but assertion is not the proper justification for reason.
APPEARS IN
संबंधित प्रश्न
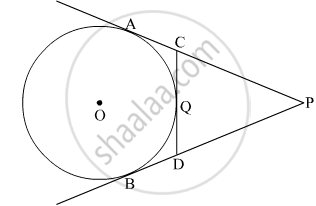
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

How many common tangents can be drawn to two circles, touching each
other externally?
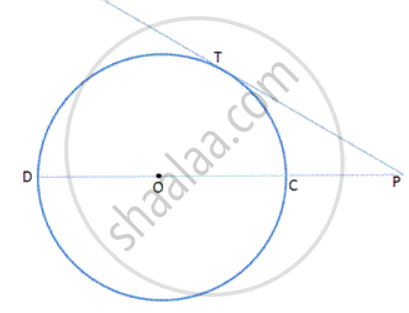
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
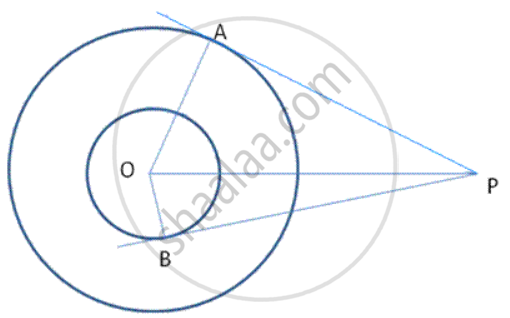
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
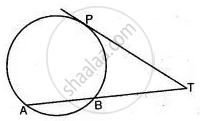
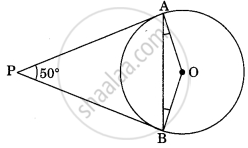
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
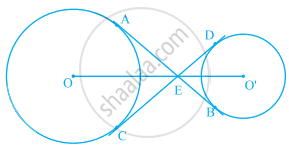
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

