Advertisements
Advertisements
प्रश्न
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
विकल्प
`sqrt7` cm
7 cm
5 cm
25 cm
उत्तर
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is 5 cm.
Explanation:
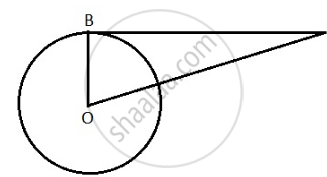
Given that AB = 4 cm, OB = 3 cm
To find OA
Applying Pythagoras theorem to triangle OAB
OB2 + AB2 = OA2
32 + 42 = OA
OA2 = 25
OA = 5 cm
Therefore the distance of A from the centre of the circle is 5 cm.
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
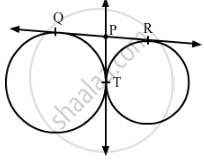
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

In the given figure, O is the centre of the circle. Find ∠CBD.

The greatest chord of a circle is called its
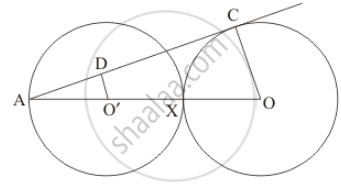
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Use the figure given below to fill in the blank:
Tangent to a circle is _______.

The ratio between the circumference and diameter of any circle is _______
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
