Advertisements
Advertisements
प्रश्न
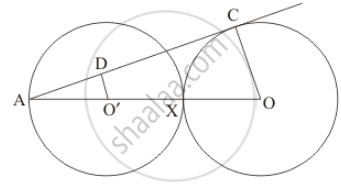
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
उत्तर
Consider the two triangles Δ ADOand Δ ACO.

We have,
∠ A is a common angle for both the triangles.
`∠ ADO =90^o` (Given in the problem)
`∠ ACO = 90^o` (Since OC is the radius and AC is the tangent to that circle at C and we know that the radius is always perpendicular to the tangent at the point of contact)
Therefore,
`∠ ADO = ∠ACO`
From AA similarity postulate we can say that,
Δ ACO ~ Δ ADO
Since the triangles are similar, all sides of one triangle will be in same proportion to the corresponding sides of the other triangle.
Consider AO′ of Δ ADO and AO of Δ ACO .
`(AO)/(AO)=(AO)/(AO+OX+OX)`
Since AO′ and O′X are the radii of the same circle, we have,
AO′ = O′X
Also, since the two circles are equal, the radii of the two circles will be equal. Therefore,
AO′ = XO
Therefore we have
`(AO)/(AO)=(AO)/(AO+AO+AO)`
`(AO)/(AO)=1/3`
Since Δ ACO ~ Δ ADO,
`(AO)/(AO)=(DO)/(CO)`
We have found that,
`(AO)/(AO)=1/3`
Therefore,
`(DO)/(CO)=1/3`
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

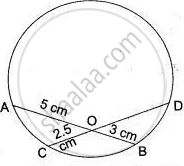
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a sector.

