Advertisements
Advertisements
प्रश्न
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
उत्तर
Given: ΔABC is inscribed in a circle. Bisector of ∠A and perpendicular bisector of BC intersect at point Q.
To prove: A, B, Q and C are con-cyclic.
Construction: Join BQ and QC.
Proof: We have assumed that, Q lies outside the circle.
In ΔBMQ and ΔCMQ,
BM = CM ...[QM is the perpendicular bisector of BC]
∠BMQ = ∠CMQ ...[Each 90°]
MQ = MQ ...[Common side]
∴ ΔBMQ ≅ ΔCMQ ...[By SAS congruence rule]
∴ BQ = CQ [By CPCT] ...(i)
Also, ∠BAQ = ∠CAQ [Given] ...(ii)
From equations (i) and (ii),
We can say that Q lies on the circle ...[Equal chords of a circle subtend equal angles at the circumference]
Hence, A, B, Q and C are con-cyclic.
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
A line through the point of contact and passing through centre of the circle is known as ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.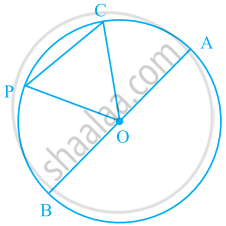
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
