Advertisements
Advertisements
प्रश्न
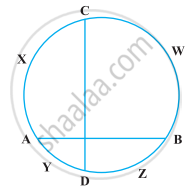
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
उत्तर
Given: In a circle AYDZBWCX, two chords AB and CD intersect at right angles.
To prove: arc CXA + arc DZB = arc AYD + arc BWC = Semi-circle.
Construction: Draw a diameter EF parallel to CD having centre M.
Proof: Since, CD || EF
arc EC = arc PD ...(i)
arc ECXA = arc EWB [Symmetrical about diameter of a circle]
arc AF = arc BF ...(ii)
We know that, ar ECXAYDF = Semi-circle
arc EA + arc AF = Semi-circle
⇒ arc EC + arc CXA = arc FB = Semi-circle ...[From equation (ii)]
⇒ arc DF + arc CXA + arc FB = Semi-circle ...[From equation (i)]
⇒ arc DF + arc FB + arc CXA = Semi-circle
⇒ arc DZB + arc C × A = Semi-circle
We know that, circle divides itself in two semi-circles, therefore the remaining portion of the circle is also equal to the semi-circle.
∴ arc AYD + arc BWC = Semi-circle
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
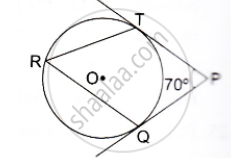
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Twice the radius is ________________
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
