Advertisements
Advertisements
प्रश्न
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
उत्तर
Given AD = 23 cm
AB = 29 cm
∠B = 90°
DS = 5cm
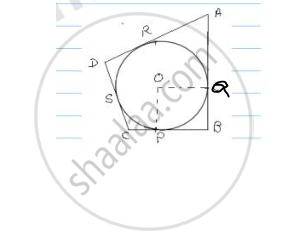
From fig in quadrilateral POQB
∠OPB = ∠OQB = 90° = ∠B = ∠POQ
and PO = OQ. ∴ POQB is a square PB = BQ = r
We know that
Tangents drawn from external point to circle are equal in length.
We know that
Tangents drawn from external point to circle are equal in length.
From A, AR = AQ …. (i)
From B, PB = QB …. (ii)
From C, PC = CS …. (iii)
From D, DR = DS …. (iv)
(i) + (ii) + (iv) ⇒ AR + DB + DR = AQ + QB + DS
⇒ (AR + DR) + r = (AQ + QB) + DS
AD + r = AB + DS
⇒ 23 + r = 29 + 5
⇒ r = 34 – 23 = 11 cm
∴ radius = 11 cm
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
The greatest chord of a circle is called its
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
