Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
рдЙрддреНрддрд░
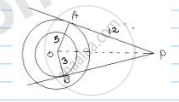
OA = 5 cm
OB = 3 cm
AP = 12 cm
BP = ?
We know that
At the point of contact, radius is perpendicular to tangent.
For circle 1, ΔOAP is right triangle
By Pythagoras theorem, ЁЭСВЁЭСГ2 = ЁЭСВЁЭР┤2 + ЁЭР┤ЁЭСГ2
⇒ ЁЭСВЁЭСГ2 = 52 + 122 = 25 + 144
= 169
⇒ OP = `sqrt(169)` = 13 ЁЭСРЁЭСЪ
For circle 2, ΔOBP is right triangle by Pythagoras theorem,
ЁЭСВЁЭСГ2 = ЁЭСВЁЭР╡2 + ЁЭР╡ЁЭСГ2
132 = 32 + ЁЭР╡ЁЭСГ2
ЁЭР╡ЁЭСГ2 = 169 − 9 = 160
ЁЭР╡ЁЭСГ = `sqrt(160) = 4sqrt(10)` ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
Prove that the tangents at the extremities of any chord make equal angles with the chord.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
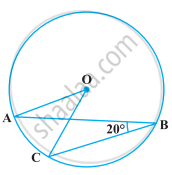
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
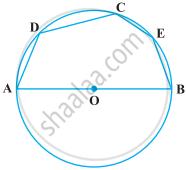
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
