Advertisements
Advertisements
प्रश्न
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
Let AOB be the diameter of the circle.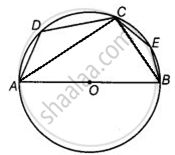
Given: ∠ADC = 120°
Firstly, join CB.
Then, we have a cyclic quadrilateral ABCD.
Since sum of opposite angles of cyclic quadrilateral is 180°, therefore
∠ADC + ∠ABC = 180°
⇒ 120° + ∠ABC = 180°
⇒ ∠ABC = 180° – 120°
⇒ ∠ABC = 60°
Now join AC.
Also, diameter subtends a right angle to the circle,
∴ In ΔABC, ∠ACB = 90°
Now, by angle sum property of a triangle, sum of all angles of a triangle is 180°.
∴ ∠CAB + ∠ABC + ∠ACB = 180°
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – 90° – 60°
⇒ ∠CAB = 30°
APPEARS IN
संबंधित प्रश्न
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
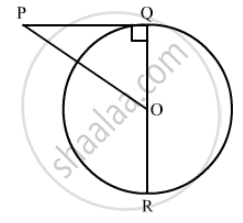
Use the figure given below to fill in the blank:
R is the _______ of the circle.

State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure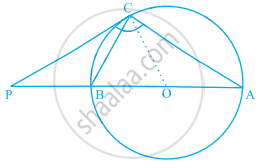
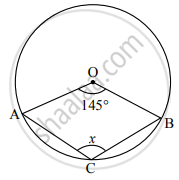
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.