Advertisements
Advertisements
प्रश्न
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
उत्तर
Let AXB and CYD are arcs of a circle whose centre and radius are O and r, respectively.

So, OA = OB = OC = OD = r ...(i)
∵ `bar(AXB) ≅ bar(CYD)`
∴ ∠AOB = ∠COD ...(ii) [Congruent arcs of a circle subtend equal angles at the centre]
In ΔAOB and ΔCOD,
AO = CO ...[From (i)]
BO = DO ...[From (i)]
∠AOB = ∠COD ...[From (ii)]
∴ ΔAOB ≅ ΔCOD ...[By SAS congruency]
`\implies` AB = CD ...[By C.P.C.T.]
`\implies (AB)/(CD) = 1`
Hence, the ratio of AB and CD is 1 : 1.
APPEARS IN
संबंधित प्रश्न
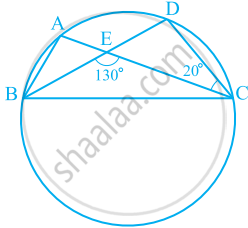
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
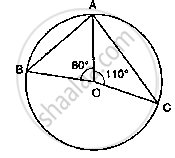
In the below fig. O is the centre of the circle. Find ∠BAC.
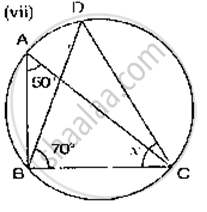
If O is the centre of the circle, find the value of x in the following figure
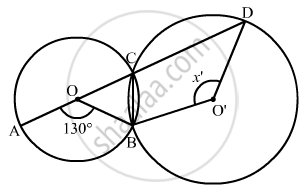
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
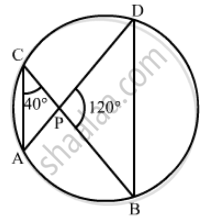
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
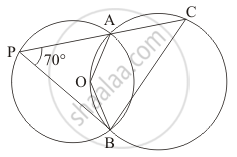
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
