Advertisements
Advertisements
प्रश्न
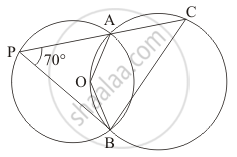
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
उत्तर
Consider the smaller circle whose centre is given as ‘O’.
The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.
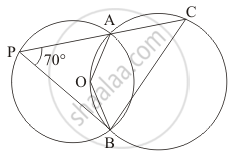
So, here we have
`angle AOB = 2 angle APB `
= 2 (70°)
`angle AOB = 140°`
Now consider the larger circle and the points ‘A’, ‘C’, ‘B’ and ‘O’ along its circumference. ‘ACBO’ form a cyclic quadrilateral.
In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to 180°.
`angleAOB + angle ACB` = 180°
`angle ACB = 180° - angle AOB`
`= 180° - 140°`
`angle ACB = 40°`
Hence ,the measure of` ` angle ACB ` is 40° .
APPEARS IN
संबंधित प्रश्न
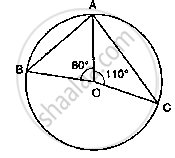
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
A chord of a circle is equal to its radius. Find the angle subtended by this chord at a point in major segment.
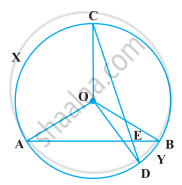
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).