Advertisements
Advertisements
प्रश्न
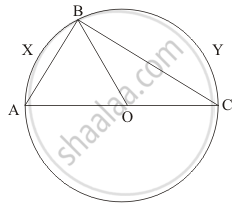
In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.
Advertisements
उत्तर
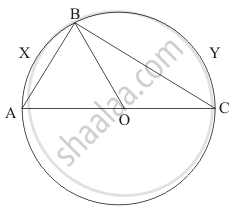
Since, O is the circumcentre of \[\bigtriangleup ABC\], So, O would be centre of the circle passing through points A, B and C.
As OA = OB (Radii of the same circle)
\[\therefore \angle OAB = \angle OBA \left( \text{ Angle opposite to equal sides are equal } \right)\]
\[\text{ or } , \angle BAC = \angle OBA\]
\[\text{ From } \left( 1 \right)\]
\[\angle BAC + \angle OBC = 90°\]
APPEARS IN
संबंधित प्रश्न
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Given an arc of a circle, complete the circle.
If O is the centre of the circle, find the value of x in the following figure
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Prove that the angle in a segment greater than a semi-circle is less than a right angle.
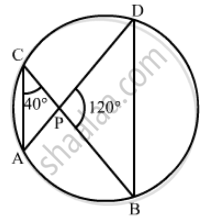
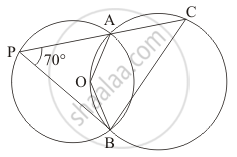
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.
If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
In the following figure, ∠ACB = 40º. Find ∠OAB.
