Advertisements
Advertisements
प्रश्न
In the given figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.

उत्तर
Let us first consider the triangle ΔABQ.
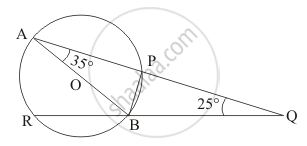
It is known that in a triangle the sum of all the interior angles add up to 180°.
So here in our triangle ΔABQ we have,
= 180° - 35° - 25°
By a property of the circle we know that an angle formed in a semi-circle will be 90°..
In the given circle since ‘AB’ is the diameter of the circle the angle
So, we have
Now considering the triangle ΔAPB we have,
= 180° - 90° - 35 °
From the given figure it can be seen that,
= 120°- 55°
Now, we can also say that,
=180° - 65 °
Hence the measure of the angle
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
If O is the centre of the circle, find the value of x in the following figure

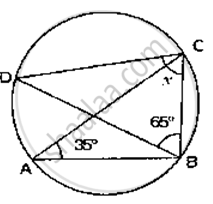
If O is the centre of the circle, find the value of x in the following figure
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
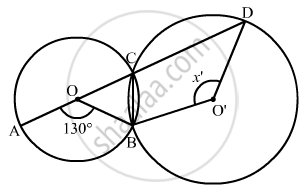
In the given figure, O and O' are centres of two circles intersecting at B and C. ACD is a straight line, find x.
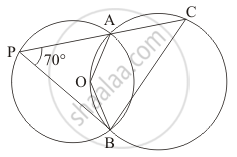
In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In a circle, the major arc is 3 times the minor arc. The corresponding central angles and the degree measures of two arcs are
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
