Advertisements
Advertisements
प्रश्न
In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

उत्तर
It is given that ‘ABCD’ is a parallelogram. But since ‘A’ is the centre of the circle, the lengths of ‘AB’ and ‘AD’ will both be equal to the radius of the circle.
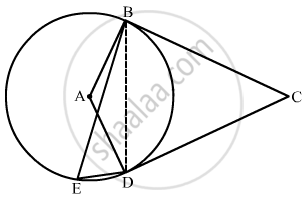
So, we have AB = AD .
Whenever a parallelogram has two adjacent sides equal then it is a rhombus.
So ‘ABCD’ is a rhombus.
Let `angleBDE = x° `.
We know that in a circle the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.
By this property we have
`angleBAD = 2 (angleBDE )`
`angleBAD = 2 x°`
In a rhombus the opposite angles are always equal to each other.
So, `angleBAD = angleBCE = 2x°`
Since the sum of all the internal angles in any triangle sums up to 180° in triangle ΔBEC , we have
`angleEBC + angleABE = angleEBC` = 180°
`angleEBC = 180° - angleBEC - angle BCE`
= 180° - x° -2x°
`angleEBS` = 180° - 3x°
In the rhombus ‘ABCD’ since one pair of opposite angles are ‘2x° ’ the other pair of opposite angles have to be (180° - 2x°)
From the figure we see that,
`angleEBC + angle ABE = angleABC `
`angleABE = angleABC - angleEBC `
= 180° - 2x° - (180° - 3x°)
`angleABE` = x°
So now we can write the required ratio as,
`(angleBCD)/(angleABE) = (2x°)/(x°)`
`(angleBCD)/(angleABE) = 2/1`
Hence the ratio between the given two angles is 2: 1 .
APPEARS IN
संबंधित प्रश्न
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
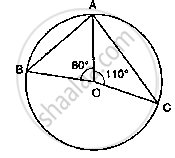
In the below fig. O is the centre of the circle. Find ∠BAC.
If O is the centre of the circle, find the value of x in the following figure
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
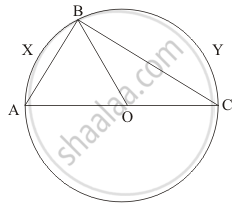
The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
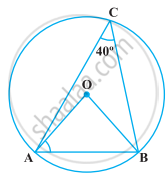
In the following figure, ∠ACB = 40º. Find ∠OAB.
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
