Advertisements
Advertisements
प्रश्न
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
उत्तर
Draw a circle having centre O. Let AB = 2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
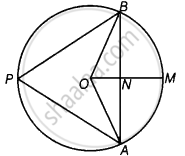
To prove: ∠APB = 45°
Here, AN = NB = 1 cm
And OB = `sqrt(2)` cm
In ΔONB, OB2 = ON2 + NB2 ...[Use Pythagoras theorem]
⇒ `(sqrt(2))^2 = ON^2 + (1)^2`
⇒ ON2 = 2 – 1 = 1
⇒ ON = 1 cm ...[Taking positive square root, because distance is always positive]
Also, ∠ONB = 90° ...[ON is the perpendicular bisector of the chord AB]
∴ ∠NOB = ∠NBO = 45°
Similarly, ∠AON = 45°
Now, ∠AOB = ∠AON + ∠NOB
= 45° + 45°
= 90°
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
∴ `∠APB = 1/2 ∠AOB`
= `90^circ/2`
= 45°
Hence proved.
APPEARS IN
संबंधित प्रश्न
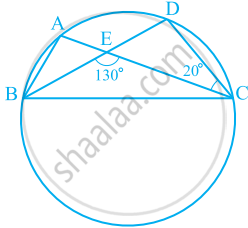
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
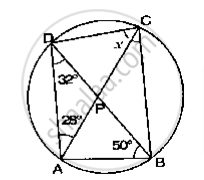
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
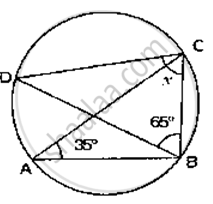
If O is the centre of the circle, find the value of x in the following figure
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, two circles intersect at A and B. The centre of the smaller circle is Oand it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
In the given figure, two congruent circles with centres O and O' intersect at A and B. If ∠AOB = 50°, then find ∠APB.

In the given figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.

In the given figure, if O is the circumcentre of ∠ABC, then find the value of ∠OBC + ∠BAC.

